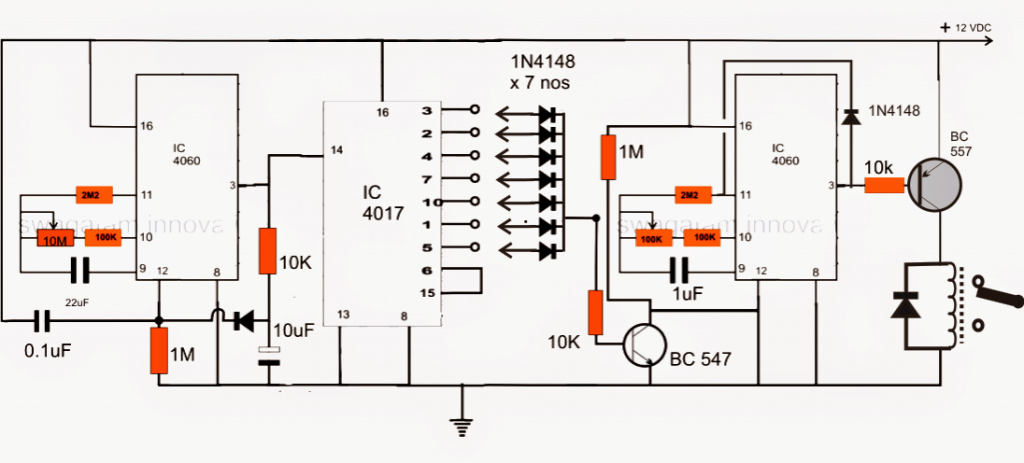
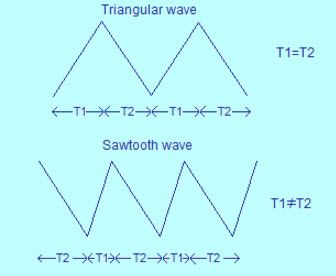
బైనరీ అదనంగా & వ్యవకలనం దశాంశ సంఖ్య వ్యవస్థతో సమానంగా ఉంటుంది. కానీ ఈ రెండింటి మధ్య ప్రధాన వ్యత్యాసం ఏమిటంటే, బైనరీ సంఖ్య వ్యవస్థ 0 & 1 వంటి రెండు అంకెలను ఉపయోగిస్తుంది, అయితే దశాంశ సంఖ్య వ్యవస్థ 0 నుండి 9 వరకు అంకెలను ఉపయోగిస్తుంది మరియు దీని ఆధారం 10. బైనరీ సిస్టమ్ కోసం కొన్ని నిర్దిష్ట నియమాలు ఉన్నాయి. మేము బైనరీ సంఖ్యలను జోడించినప్పుడు మరియు తీసివేసినప్పుడు మాదిరిగానే అప్పులు తీసుకునేటప్పుడు చాలా జాగ్రత్తగా ఉండాలి ఎందుకంటే ఇవి చాలా తరచుగా జరుగుతాయి. ఈ వ్యాసం బైనరీ సంఖ్యల సంకలనం & వ్యవకలనం యొక్క అవలోకనాన్ని క్రింద వివరంగా చర్చిస్తుంది.
బైనరీ చేరిక & వ్యవకలనం అంటే ఏమిటి?
-1101 వంటి 5-బిట్ సంఖ్యలను నిర్వహించడంలో కంప్యూటర్ సాధించినట్లయితే, ఇక్కడ మైనస్ సైన్ బిట్ మరియు మిగిలిన అంకెలు మాగ్నిట్యూడ్ బిట్స్ అయితే ఈ 5-బిట్ సంఖ్యను 11101 లాగా సూచించవచ్చు. ఇక్కడ ఈ అంకెలో, మొదటి అంకె '1' ప్రతికూల చిహ్నాన్ని నిర్దేశిస్తుంది మరియు మిగిలిన 4 అంకెలు సంఖ్యల పరిమాణం.
అదే విధంగా, 01101 +1101 బైనరీ సంఖ్యలను సూచిస్తుంది.
సంఖ్య 1 యొక్క పూరక పరిమాణం యొక్క భావనను ఉపయోగించి ప్రతికూల (-) సంఖ్యను కూడా సూచిస్తారు.
కాబట్టి బైనరీ సంఖ్య - 1101 ను 10010 గా సూచించవచ్చు, ఇక్కడ మొదటి అంకె చాలా ముఖ్యమైన బిట్ లేదా MSB. దీని అర్థం ప్రతికూల సంఖ్య మరియు 0010 అనేది 1 యొక్క పరిమాణం.
అదే విధంగా, 11011 0100 వంటి సంఖ్యను పేర్కొంటుంది.
అదేవిధంగా, 2 యొక్క పూరక పద్ధతి –ve బైనరీ సంఖ్యను సూచించడానికి కూడా ఉపయోగించబడుతుంది.
ప్రతికూల సంఖ్యలను సూచించే సైన్ బిట్ను ఉపయోగించి బైనరీ అదనంగా & వ్యవకలనం పద్ధతులు కంప్యూటర్ రూపకల్పనలో మొత్తాలను లెక్కించడానికి మరియు అదనపు ప్రక్రియ ద్వారా మాత్రమే బైనరీ సంఖ్యల తేడాలను సులభంగా ఉపయోగిస్తాయి.
బైనరీ చేరిక
బైనరీ సంకలన సాంకేతికత దశాంశ సంఖ్యల సాధారణ చేరికతో సమానంగా ఉంటుంది, ఇది 10 అంకెల ప్రత్యామ్నాయ విలువగా, ఇది 2 విలువను కలిగి ఉంటుంది.
ఉదాహరణకు, మేము 7 + 9 ను మానవీయంగా గణించినప్పుడు, సమాధానం 16. కాబట్టి ఫలితం 1 మరియు 6 వంటి రెండు అంకెలు లాగా వ్రాయవలసి ఉంటుందని మనకు తెలుసు. 1 6 వంటి ఫలితాన్ని వ్రాయడానికి ప్రధాన కారణం, 7 యొక్క అదనంగా + 9 సింగిల్ డిజిట్ కంటే ఎక్కువ. కాబట్టి ఫలితాన్ని ఒకే అంకె ద్వారా సూచించలేము ఎందుకంటే అతిపెద్ద సింగిల్ డిజిట్ ‘9’.
అదేవిధంగా, మేము రెండు బైనరీ సంఖ్యలను సంకలనం చేయాలనుకున్నప్పుడు, ఉత్పత్తి 1 కంటే పెద్దదిగా ఉంటే మాత్రమే మనకు క్యారీ ఉంటుంది, ఎందుకంటే బైనరీ సంఖ్యలలో 1 అత్యధిక సంఖ్య. బైనరీ అదనంగా నియమాలు వ్యవకలనం యొక్క క్రింది సత్య పట్టికలో ఇవ్వబడ్డాయి.
TO | బి | A + B. | తీసుకువెళ్ళండి |
0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 1 |
పై పట్టిక రూపంలో, ప్రారంభ మూడు సమీకరణాలు బైనరీ అంకెల సంఖ్యకు సమానంగా ఉంటాయి. దశల వారీగా బైనరీ సంఖ్యల కలయిక వివరంగా వివరించబడింది. బైనరీ అదనంగా 11011 & 10101 యొక్క ఉదాహరణ తీసుకోండి.
1 1 1 1 (క్యారీ)
1 1 0 1 1 (27)
(+) 1 0 1 0 1 (21)
_ _ _ _ _ _ _ _ _ _
1 1 0 0 0 0 (48)
ఇక్కడ దశల వారీ బైనరీ అదనంగా నియమాలు క్రింద వివరించబడ్డాయి
1 + 1 => 1 0, కాబట్టి క్యారీ 1 తో 0
1 + 1 + 0 => 1 0. కాబట్టి క్యారీ 1 తో 0
1 + 0 + 1 => 10 => 0. కాబట్టి క్యారీ -1 తో 0
క్యారీ -1 తో 1 + 1 + 0 => 10 => 10 = 0
క్యారీ -1 తో 1 + 1 + 1 => 10 + 1 => 11 = 1
1 +1 +1 = 11
10 + 1 => 11 మరియు ఇది 2 + 1 = 3 కు సమానం అని జాగ్రత్తగా గమనించండి. అందువల్ల అవసరమైన ఫలితం 111000.
ఉదాహరణలు
ది బైనరీ అదనంగా ఉదాహరణలు కింది చిత్రంలో చూపబడ్డాయి.

బైనరీ-అదనంగా
బైనరీ వ్యవకలనం: మొదటి పద్ధతి
వ్యవకలనంలో, ఇది ప్రాథమిక సాంకేతికత. ఈ పద్ధతిలో, తీసివేసే సంఖ్య పెద్ద సంఖ్య నుండి చిన్నదిగా ఉండాలి అని నిర్ధారించుకోండి, లేకపోతే ఈ సాంకేతికత తగిన విధంగా పనిచేయదు.
మినియెండ్ సబ్ట్రాహెండ్ కంటే చిన్నదిగా ఉంటే, అప్పుడు వారి స్థానాలను మార్చుకుని, ప్రభావం -ve సంఖ్యగా ఉంటుందని గుర్తుంచుకోవడం ద్వారా ఈ పద్ధతి ఉపయోగించబడుతుంది. బైనరీ వ్యవకలనం నియమాలు వ్యవకలనం యొక్క క్రింది సత్య పట్టికలో ఇవ్వబడ్డాయి.
| TO | బి | ఎ-బి | రుణం |
0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
ఉదాహరణకు, బైనరీ వ్యవకలనంలో, మిన్యూండ్ నుండి సబ్ట్రాహెండ్ను తీసివేయండి. సబ్ట్రాహెండ్ (110112) మరియు మినియుండ్ (11011012) యొక్క ఉదాహరణను తీసుకోండి. వ్యవకలనం కోసం, సబ్ట్రాహెండ్ లాగా ఈ రెండింటిని అమర్చండి. దీనికి ఉదాహరణ క్రింద ఇవ్వబడింది.
1101101
- 11011
సబ్ట్రాహెండ్లో అదే సంఖ్యలో అంకెలను పొందడానికి, అవసరమైన చోట సున్నాలను జోడించండి.
1101101
- 0011011
_ _ _ _ _ _ _ _
1010010
పై బైనరీ వ్యవకలన ఉదాహరణలో, పైన చూపిన పట్టిక రూపం సహాయంతో వ్యవకలనం కుడి వైపు నుండి ఎడమ వైపుకు సాధించబడింది. ఇక్కడ దశల వారీ బైనరీ వ్యవకలనం నియమాలు క్రింద వివరించబడ్డాయి.
ఇన్పుట్ 1 1 = 0 అయితే, తదుపరి దశకు రుణం 0.
ఇన్పుట్ 0 1 = 1 & రుణం 0. అయితే 1 0 = 1 తరువాత దశకు రుణం 1.
ఇన్పుట్ 1 0 = 0 & రుణం ఉంటే. కాబట్టి 1 1 = 0 తరువాత తదుపరి దశకు రుణం 0.
ఇన్పుట్ 1 1 = 0 & రుణం 0. అయితే 0 0 = 0 తరువాత దశకు రుణం 0.
ఇన్పుట్ 0 1 = 1 & రుణం 0. అయితే 1 0 = 1 తరువాత దశకు రుణం 1.
ఇన్పుట్ 1 0 = 1 & రుణం 1. అయితే 1 1 = 0, తరువాత దశకు రుణం 0.
చివరి దశ, ఇన్పుట్ 1 0 = 0 & రుణం 0. అయితే 10 = 1, తరువాత దశకు రుణం 0.
కాబట్టి తుది ఫలితం 1010010 అవుతుంది
రెండవ పద్ధతి: రెండు కాంప్లిమెంట్
మొదట, సబ్ట్రాహెండ్ మరియు మినియెండ్స్లోని అంకెలు సమానంగా ఉండాలని నిర్ధారించండి. పై ఉదాహరణలో, మినియెండ్స్లోని అంకెలు 7 అయితే సబ్ట్రాహెండ్లో అంకెలు 5 ఉన్నాయి. కాబట్టి మనం సున్నాలను జోడించడం ద్వారా సబ్ట్రాహెండ్లోని అంకెలను విస్తరించాలి. సంఖ్య యొక్క 2 యొక్క పూరక సంఖ్య యొక్క ప్రతి అంకెను సున్నా వంటి వాటికి మరియు సున్నాలకు పూర్తి చేయడం ద్వారా సాధించవచ్చు. చివరగా, ఒకరి పూరకానికి ఒకదాన్ని జోడించండి. ఈ రెండింటి పూరకానికి ఉదాహరణ క్రింద చూపబడింది.
0011011
0 ని 1 కి మరియు 1 ని 0 కి మార్చడం ద్వారా 1 యొక్క పూరకం సాధించవచ్చు. కాబట్టి ఫలితం క్రింది విధంగా ఉంటుంది.
0011011 - - - -> 1100100 (1 యొక్క పూరక)
1 నుండి 1 యొక్క పూరకాన్ని జోడించడం ద్వారా 2 యొక్క పూరకం సాధించవచ్చు. కాబట్టి ఫలితం క్రింది విధంగా ఉంటుంది.
1100100
+ 0000001
_ _ _ _ _ _ _ _
= 1100101
ఇప్పుడు సబ్ట్రాహెండ్ యొక్క 2 యొక్క పూరక & మినియెండ్ను జోడించండి.
1101101 (సబ్ట్రాహెండ్)
+ 1100101 (2 యొక్క పూరక)
_ _ _ _ _ _ _ _
(ఎంఎస్బి) (1) 1010010
పై ఫలితంలో, ఫలితం యొక్క MSB (చాలా ముఖ్యమైన బిట్) ను విస్మరించండి. అదనపు బిట్ లేకపోతే, అంకెలను జోడించేటప్పుడు మీరు పొరపాటు చేసారు.
ఉదాహరణలు
ది బైనరీ వ్యవకలనం ఉదాహరణలు కింది చిత్రంలో చూపబడ్డాయి.

బైనరీ-వ్యవకలనం
అందువల్ల, ఇదంతా బైనరీ సంకలనం యొక్క అవలోకనం మరియు వ్యవకలనం , ఇందులో బైనరీ అదనంగా, బైనరీ అదనంగా నియమాలు, బైనరీ అదనంగా ఉదాహరణలు మరియు బైనరీ వ్యవకలనం, బైనరీ వ్యవకలనం నియమాలు, బైనరీ వ్యవకలనం ఉదాహరణలు ఉన్నాయి. ఇక్కడ మీ కోసం ఒక ప్రశ్న ఉంది, బైనరీ అదనంగా మరియు వ్యవకలనం మధ్య ఉన్న తేడా ఏమిటి?