గాస్ లా అంటే ఏమిటి: థియరీ & దాని ప్రాముఖ్యత

విజ్ఞాన పరిధి విస్తృతంగా అభివృద్ధి చెందుతోంది మరియు వివిధ పరిణామాలు మరియు సాంకేతికతలతో చేర్చబడినందున, మనం ఎంత ఎక్కువ నేర్చుకుంటామో మనం జ్ఞానాన్ని పొందుతాము. మరియు మనం తెలుసుకోవలసిన ఒక కీలకమైన అంశం గాస్ చట్టం, ఇది ఉపరితలం మరియు భావనకు అదనంగా విద్యుత్ ఛార్జీని విశ్లేషిస్తుంది విద్యుత్ ప్రవాహం . ఈ చట్టం మొదట 1773 లో లాగ్రేంజ్ చేత వ్యక్తీకరించబడింది మరియు తరువాత దీనిని 1813 లో ఫ్రెడరిక్ మద్దతు ఇచ్చాడు. ఈ చట్టం మాక్స్వెల్ ప్రతిపాదించిన నాలుగు సమీకరణాలలో ఒకటి, ఇక్కడ ఇది క్లాసికల్ ఎలక్ట్రోడైనమిక్స్కు ప్రాథమిక భావన. కాబట్టి, భావనలో మరింత మునిగిపోదాము మరియు గాస్ చట్టం యొక్క అన్ని సంబంధిత అంశాలను తెలుసుకుందాం.

గాస్ చట్టం అంటే ఏమిటి?

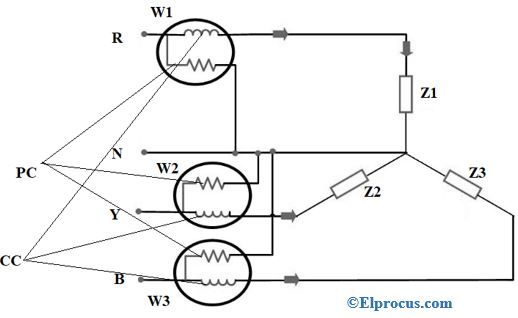
అయస్కాంత మరియు విద్యుత్ ప్రవాహాల యొక్క రెండు భావనలలో గాస్ చట్టాన్ని నిర్వచించవచ్చు. విద్యుత్తు దృష్టిలో, పరివేష్టిత ఉపరితలం గుండా విద్యుత్ ప్రవాహం మొత్తం విద్యుత్ చార్జీకి ప్రత్యక్ష నిష్పత్తిని కలిగి ఉందని ఈ చట్టం నిర్వచిస్తుంది. ఇన్సులర్ ఎలక్ట్రికల్ ఛార్జీలు ఉన్నాయని ఇది సూచిస్తుంది మరియు ఇలాంటి ఛార్జీలు తిప్పికొట్టబడతాయి, అయితే అసమాన ఛార్జీలు ఆకర్షించబడతాయి. మరియు అయస్కాంతత్వం యొక్క దృష్టాంతంలో, పరివేష్టిత ఉపరితలం గుండా అయస్కాంత ప్రవాహం శూన్యమని ఈ చట్టం పేర్కొంది. మరియు వేరు చేయబడిన పరిశీలనలో గాస్ చట్టం స్థిరంగా ఉన్నట్లు అనిపిస్తుంది అయస్కాంత ధ్రువాలు ఉనికి లేకపోవుట. ది గాస్ లా రేఖాచిత్రం క్రింద చూపబడింది:

గాస్ లా రేఖాచిత్రం

పరివేష్టిత ఉపరితలంలోని నికర విద్యుత్ ప్రవాహం పర్మిటివిటీకి అనుగుణంగా విద్యుత్ చార్జీకి సమానం అని ఈ చట్టాన్ని నిర్వచించవచ్చు.

ఎఫ్_{విద్యుత్}= Q / is₀

మూసివేసిన ఉపరితలం లోపల మొత్తం విద్యుత్ చార్జీకి ‘Q’ అనుగుణంగా ఉంటుంది

'ఉంది₀’విద్యుత్ స్థిరమైన కారకానికి అనుగుణంగా ఉంటుంది

ఇది ప్రాథమికమైనది గాస్ లా ఫార్ములా .

గాస్ లా డెరివేషన్

గాస్ చట్టం కూలంబ్ యొక్క చట్టం యొక్క సంబంధిత భావనగా పరిగణించబడుతుంది, ఇది బహుళ ఆకృతీకరణల యొక్క విద్యుత్ క్షేత్రాన్ని అంచనా వేయడానికి అనుమతిస్తుంది. ఈ చట్టం ఉపరితలం అంతటా స్థలాన్ని సృష్టించే విద్యుత్ క్షేత్ర రేఖలతో పరస్పర సంబంధం కలిగి ఉంటుంది, ఇది విద్యుత్ చార్జ్ ‘క్యూ’ అంతర్గత ఉపరితలంపై కప్పబడి ఉంటుంది. కౌలాంబ్ యొక్క చట్టం యొక్క కుడి వైపున ఉన్న గాస్ చట్టం ఈ క్రింది విధంగా ప్రాతినిధ్యం వహిస్తుందని అనుకుందాం:

ఇ = (1 / (4∏є₀)). (Q / r^{రెండు})

ఇక్కడ EA = Q /₀

పై వాటిలో గాస్ లా గణిత వ్యక్తీకరణ , ‘A’ 4∏ r అయిన విద్యుత్ చార్జ్‌ను కలుపుతున్న నికర ప్రాంతానికి అనుగుణంగా ఉంటుంది^{రెండు}. గాస్ చట్టం మరింత వర్తిస్తుంది మరియు ఎలక్ట్రిక్ ఛార్జ్ లైన్లు ఉపరితలంపై లంబంగా అమర్చబడినప్పుడు పనిచేస్తాయి, ఇక్కడ ‘Q’ పరివేష్టిత ఉపరితలానికి అంతర్గత విద్యుత్ చార్జీకి అనుగుణంగా ఉంటుంది.

ఉపరితలం యొక్క కొంత భాగాన్ని మూసివేసిన ఉపరితలానికి లంబ కోణ స్థానం వద్ద సమలేఖనం చేయనప్పుడు, అప్పుడు కాస్ యొక్క కారకం కలిసిపోతుంది, ఇది విద్యుత్ క్షేత్ర రేఖలు ఉపరితలానికి సమాంతర స్థితిలో ఉన్నప్పుడు శూన్యంగా కదులుతుంది. ఇక్కడ, పరివేష్టిత అనే పదం ఉపరితలం ఎలాంటి ఖాళీలు లేదా రంధ్రాల నుండి విముక్తి పొందాలని సూచిస్తుంది. ‘EA’ అనే పదం విద్యుత్ ప్రవాహాన్ని సూచిస్తుంది, ఇది ఉపరితలం కాకుండా వేరుగా ఉన్న మొత్తం విద్యుత్ లైన్లతో సంబంధం కలిగి ఉంటుంది. పై భావన వివరిస్తుంది గాస్ లా ఉత్పన్నం .

గాస్ చట్టం అనేక పరిస్థితులకు వర్తిస్తుంది కాబట్టి, విద్యుత్ క్షేత్రంలో పెరిగిన సమరూప స్థాయిలు ఉన్నప్పుడు చేతి లెక్కలు చేయడం ప్రధానంగా ప్రయోజనకరంగా ఉంటుంది. ఈ సందర్భాలలో స్థూపాకార సమరూపత మరియు గోళాకార సమరూపత ఉన్నాయి. ది గాస్ లా SI యూనిట్ ప్రతి కూలంబ్‌కు న్యూటన్ మీటర్లు స్క్వేర్డ్, ఇది N మీ^{రెండు}సి^-1.

డైలెక్ట్రిక్స్లో గాస్ లా

ఒక కోసం విద్యుద్వాహక పదార్ధం , ధ్రువణత కారణంగా ఎలెక్ట్రోస్టాటిక్ ఫీల్డ్ వైవిధ్యంగా ఉంటుంది, ఎందుకంటే ఇది శూన్యంలో కూడా భిన్నంగా ఉంటుంది. కాబట్టి, గాస్ చట్టం ఇలా సూచించబడుతుంది

E = ρ /₀

ఇది శూన్యంలో కూడా వర్తిస్తుంది మరియు విద్యుద్వాహక పదార్ధం కోసం పున ons పరిశీలించబడుతుంది. దీనిని రెండు విధానాలలో చిత్రీకరించవచ్చు మరియు అవి అవకలన మరియు సమగ్ర రూపాలు.

మాగ్నెటోస్టాటిక్స్ కోసం గాస్ లా

విద్యుత్ క్షేత్రాల నుండి వైవిధ్యంగా ఉండే అయస్కాంత క్షేత్రాల యొక్క ప్రాథమిక భావన చుట్టుపక్కల ఉచ్చులను ఉత్పత్తి చేసే క్షేత్ర రేఖలు. దక్షిణ మరియు ఉత్తర ధ్రువాలను వేరు చేయడానికి అయస్కాంతం సగం గా గమనించబడదు.

ఇతర విధానం ఏమిటంటే, అయస్కాంత క్షేత్రాల దృష్టిలో, పరివేష్టిత (గాస్సియన్) ఉపరితలం గుండా వెళ్ళే మొత్తం అయస్కాంత ప్రవాహం శూన్యమని గమనించడం చాలా సులభం. ఉపరితలంపై అంతర్గతంగా కదిలే విషయం బయటపడాలి. మాగ్నెటోస్టాటిక్స్ కోసం గాస్ చట్టాన్ని ఇది సూచిస్తుంది

ʃB.dS = 0 = dHds cosϴ = 0

దీనిని మాగ్నెటిక్ ఫ్లక్స్ పరిరక్షణ సూత్రం అని కూడా అంటారు.

µcosϴʃI = 0 ఇది ʃI = 0 అని సూచిస్తుంది

కాబట్టి, పరివేష్టిత ఉపరితలంలోకి కదిలే ప్రవాహాల నికర మొత్తం శూన్యంగా ఉంటుంది.

ప్రాముఖ్యత

ఈ విభాగం యొక్క స్పష్టమైన వివరణ ఇస్తుంది గాస్ చట్టం యొక్క ప్రాముఖ్యత .

వస్తువు యొక్క పరిమాణం లేదా ఆకృతిపై ఆధారపడకుండా ఏ రకమైన క్లోజ్డ్ ఉపరితలం కోసం గాస్ యొక్క న్యాయ ప్రకటన సరైనది.

చట్టం యొక్క ప్రాథమిక సూత్రంలో ‘క్యూ’ అనే పదం ఉపరితలం లోపలికి ఏ స్థానం ఉన్నా పూర్తిగా ఆవరించబడిన అన్ని ఛార్జీల ఏకీకరణను కలిగి ఉంటుంది.

ఒకవేళ, ఎంచుకున్న ఉపరితలం విద్యుత్ క్షేత్రం యొక్క అంతర్గత మరియు బాహ్య ఛార్జీలు రెండింటినీ కలిగి ఉంటుంది (ఎడమ స్థానంలో ఫ్లక్స్ ఉన్న చోట ‘S’ లోపల మరియు వెలుపల విద్యుత్ ఛార్జీలు ఉంటాయి).

కాస్ చట్టం యొక్క సరైన స్థానం మీద ‘q’ కారకం ‘S’ కు పూర్తి విద్యుత్ ఛార్జ్ అంతర్గతమని సూచిస్తుంది.

గాస్ చట్టం యొక్క కార్యాచరణ కోసం ఎంచుకున్న ఉపరితలాన్ని గాస్సియన్ ఉపరితలం అని పిలుస్తారు, అయితే ఈ ఉపరితలం ఎలాంటి వివిక్త ఛార్జీల ద్వారా పంపించకూడదు. ఎలక్ట్రిక్ ఛార్జ్ స్థానంలో వివిక్త ఛార్జీలు సరిగ్గా నిర్వచించబడకపోవడమే దీనికి కారణం. మీరు విద్యుత్ ఛార్జీకి దగ్గరగా ఉన్నప్పుడు, ఫీల్డ్ ఎటువంటి సరిహద్దు లేకుండా మెరుగుపడుతుంది. గాస్సియన్ ఉపరితలం నిరంతర ఛార్జ్ కేటాయింపు ద్వారా వెళుతుంది.

వ్యవస్థ కొంత సమతుల్యతను కలిగి ఉన్న దృష్టాంతంలో ఎలెక్ట్రోస్టాటిక్ క్షేత్రం యొక్క మరింత సరళీకృత విశ్లేషణ కోసం గాస్ చట్టం ప్రధానంగా ఉపయోగించబడుతుంది. తగిన గాస్సియన్ ఉపరితలం ఎంచుకోవడం ద్వారా మాత్రమే ఇది వేగవంతం అవుతుంది.

మొత్తంగా, ఈ చట్టం కూలంబ్ చట్టంలో ఉన్న స్థానం ఆధారంగా విలోమ చతురస్రంపై ఆధారపడి ఉంటుంది. గాస్ చట్టంలో ఎలాంటి ఉల్లంఘన విలోమ చట్టం యొక్క విచలనాన్ని సూచిస్తుంది.

ఉదాహరణలు

కొన్నింటిని పరిశీలిద్దాం గాస్ లా ఉదాహరణలు :

1). విద్యుత్ ప్రవాహాన్ని కొలిచే 3D ప్రదేశంలో పరివేష్టిత గాస్సియన్ ఉపరితలం. గాస్సియన్ ఉపరితలం గోళాకార ఆకారంలో 30 ఎలక్ట్రాన్లతో కప్పబడి 0.5 మీటర్ల వ్యాసార్థం కలిగి ఉంటుంది.

• ఉపరితలం గుండా వెళ్ళే విద్యుత్ ప్రవాహాన్ని లెక్కించండి
• ఉపరితల మధ్య నుండి కొలిచిన క్షేత్రానికి 0.6 మీటర్ల దూరం ఉన్న విద్యుత్ ప్రవాహాన్ని కనుగొనండి.
• పరివేష్టిత ఛార్జ్ మరియు విద్యుత్ ప్రవాహం మధ్య ఉన్న సంబంధాన్ని తెలుసుకోండి.

జవాబు a.

ఎలక్ట్రిక్ ఫ్లక్స్ యొక్క సూత్రంతో, ఉపరితలంలో జతచేయబడిన నికర ఛార్జీని లెక్కించవచ్చు. ఉపరితలంపై కనిపించే మొత్తం ఎలక్ట్రాన్లతో ఎలక్ట్రాన్ కోసం ఛార్జ్ గుణకారం ద్వారా దీనిని సాధించవచ్చు. దీనిని ఉపయోగించి, ఖాళీ స్థలం అనుమతి మరియు విద్యుత్ ప్రవాహాన్ని తెలుసుకోవచ్చు.

= = Q / is₀= [30 (1.60 * 10-¹⁹) / 8.85 * 10^-12]

= 5.42 * 10^-12న్యూటన్ * మీటర్ / కూలంబ్

సమాధానం b.

విద్యుత్ ప్రవాహం యొక్క సమీకరణాన్ని తిరిగి అమర్చడం మరియు వ్యాసార్థం ప్రకారం ప్రాంతాన్ని వ్యక్తీకరించడం విద్యుత్ క్షేత్రాన్ని లెక్కించడానికి ఉపయోగపడుతుంది.

Ф = EA = 5.42 * 10^-12న్యూటన్ * మీటర్ / కూలంబ్

ఇ = (5.42 * 10^-) / TO

= (5.42 * 10^-) / 4∏ (0.6)^{రెండు}

ఎలక్ట్రిక్ ఫ్లక్స్ పరివేష్టిత విద్యుత్ చార్జ్‌తో ప్రత్యక్ష నిష్పత్తిని కలిగి ఉన్నందున, ఉపరితలంపై విద్యుత్ చార్జ్ పెరిగినప్పుడు, దాని గుండా వెళ్ళే ఫ్లక్స్ కూడా మెరుగుపడుతుందని ఇది సూచిస్తుంది.

2). 0.12 మీటర్ల వ్యాసార్థం కలిగిన గోళాన్ని పరిగణించండి, ఇది ఉపరితలంపై ఇలాంటి ఛార్జ్ పంపిణీని కలిగి ఉంటుంది. ఈ గోళం 0.20 మీటర్ల దూరంలో ఉంచిన విద్యుత్ క్షేత్రాన్ని కలిగి ఉంది, ఇది -10 న్యూటన్లు / కూలంబ్ విలువను కలిగి ఉంటుంది. లెక్కించండి

• గోళంలో ప్రసారం చేయబడిన విద్యుత్ ఛార్జ్ మొత్తాన్ని లెక్కించాలా?
• గోళానికి అంతర్గతంగా ఉన్న విద్యుత్ క్షేత్రం ఎందుకు లేదా ఎందుకు నిర్వచించకూడదు?

జవాబు a.

Q తెలుసుకోవాలంటే, మనం ఇక్కడ ఉపయోగించే ఫార్ములా

E = Q / (4∏r^{రెండు}ఉంది₀IS)

ఈ Q = 4∏ (0.20) తో^{రెండు}(8.85 * 10^-12) (- 100)

Q = 4.45 * 10^-10సి

సమాధానం b.

ఖాళీ గోళాకార ప్రదేశంలో, ఉపరితలం వద్ద మొత్తం ఛార్జ్ నివసిస్తున్న అంతర్గతంగా విద్యుత్ ఛార్జ్ లేదు. అంతర్గత ఛార్జ్ లేనందున, గోళానికి అంతర్గతంగా ఉండే విద్యుత్ క్షేత్రం కూడా శూన్యంగా ఉంటుంది.

గాస్ లా యొక్క అనువర్తనాలు

ఈ చట్టం ఉపయోగించిన కొన్ని అనువర్తనాలు క్రింద వివరించిన విధంగా ఉన్నాయి:

• సమాంతరంగా ఉంచిన రెండు కండెన్సర్ ప్లేట్ల మధ్య విద్యుత్ క్షేత్రం E = σ / є0, ఇక్కడ ‘σ’ ఉపరితల ఛార్జ్ యొక్క సాంద్రతకు అనుగుణంగా ఉంటుంది.
• ది విద్యుత్ క్షేత్ర తీవ్రత ఇది ఛార్జ్ ఉన్న విమానం షీట్ దగ్గర ఉంచబడుతుంది E = σ / 2є₀K మరియు the ఉపరితల ఛార్జ్ యొక్క సాంద్రతకు అనుగుణంగా ఉంటాయి
• కండక్టర్ దగ్గర ఉంచిన విద్యుత్ క్షేత్ర తీవ్రత E = σ / is₀K మరియు the ఉపరితల ఛార్జ్ యొక్క సాంద్రతకు అనుగుణంగా ఉంటాయి, మాధ్యమాన్ని విద్యుద్వాహకముగా ఎన్నుకున్నప్పుడు E_గాలి= σ / ఉంది₀
• ‘R’ వ్యాసార్థంలో అనంతమైన విద్యుత్ చార్జ్ ఉంచిన సందర్భంలో, అప్పుడు E = ƴ / 2∏rє₀

గాస్సియన్ ఉపరితలాన్ని ఎన్నుకోవటానికి, విద్యుద్వాహక స్థిరాంకం మరియు విద్యుత్ ఛార్జ్ యొక్క నిష్పత్తి 2 డి ఉపరితలం ద్వారా అందించబడే రాష్ట్రాలను పరిగణనలోకి తీసుకోవాలి, ఇది ఛార్జ్ పంపిణీ యొక్క విద్యుత్ క్షేత్ర సమరూపత కంటే సమగ్రంగా ఉంటుంది. ఇక్కడ, మూడు విభిన్న పరిస్థితులు వస్తాయి:

• ఛార్జ్ కేటాయింపు స్థూపాకారంగా సుష్ట ఆకారంలో ఉన్నప్పుడు
• ఛార్జ్ కేటాయింపు గోళాకార సుష్ట ఆకారంలో ఉన్నప్పుడు
• ఇతర దృష్టాంతం ఏమిటంటే, ఛార్జ్ కేటాయింపులో విమానం ద్వారా అనువాద సమరూపత ఉంటుంది

మేము క్షేత్రాన్ని కొలవవలసిన అవసరం ఉందా అనే పరిస్థితి ఆధారంగా గాస్సియన్ ఉపరితల పరిమాణం ఎంపిక చేయబడింది. ఈ సిద్ధాంతం సంబంధిత సమరూపత ఉన్నప్పుడు ఫీల్డ్‌ను తెలుసుకోవడంలో మరింత ఉపయోగపడుతుంది ఎందుకంటే ఇది ఫీల్డ్ యొక్క దిశను సూచిస్తుంది.

మరియు ఇదంతా గాస్ లా భావన గురించి. ఇక్కడ, గాస్ చట్టం అంటే ఏమిటి, దాని ఉదాహరణలు, ప్రాముఖ్యత, సిద్ధాంతం, సూత్రం మరియు అనువర్తనాలు ఏమిటో తెలుసుకోవడానికి మేము ఒక వివరణాత్మక విశ్లేషణ ద్వారా వెళ్ళాము. అదనంగా, గురించి మరింత తెలుసుకోవడానికి ఒకటి సిఫార్సు చేయబడింది గాస్ చట్టం యొక్క ప్రయోజనాలు మరియు గాస్ చట్టం యొక్క ప్రతికూలతలు , దాని రేఖాచిత్రం మరియు ఇతరులు.